Sometimes you are asked to filter a complex set of routes using as few lines as possible. Here we will examine a way to calculate the subnet and wildcard for such a scenario. With some practice, you should be able to calculate any set in 5 minutes or less. It is also recommend to test your results in a lab setting, using loopbacks and distribute-lists.
For example, say we are asked to filter the following routes using a one-line filter:
102.17.63.0
126.22.61.0
111.22.57.0
125.33.101.0
First, make a table as shown:
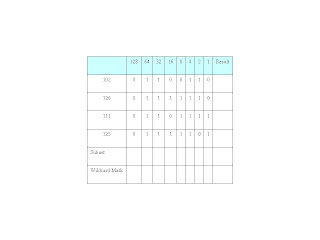
Then, enter the decimal digits from the first octet in the left-hand column. Convert each number to binary. You can use Windows Calculator set to Scientific Mode to do the conversion if you so wish.
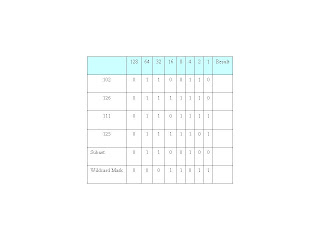
In the binary area, first check the octet then column by column, apply the following rules:
- If the entire octet is 0, the subnet is 0 for that octet, and the mask is 255 for that octet.
- Else If the column is all 0’s, the subnet is 0, and the mask is 0
- Else If the column is all 1’s, the subnet is 1, and the mask is 0
- Else the column is a mixture of 1’s and 0’s, the subnet is 0, and the mask is 1.
For the first octet the table should look like:
Convert the binary Subnet and Wildcard Mask to decimal to complete the table:
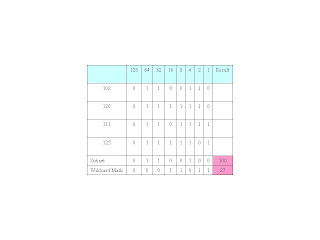
So far, our filter looks like: 100.xxx.xxx.xxx 27.xxx.xxx.xxx
For the second octet the completed table should look like:
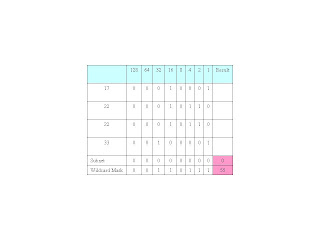
Our summary address now looks like: 100.0.xxx.xxx 27.55.xxx.xxx
For the third octet the completed table should look like:
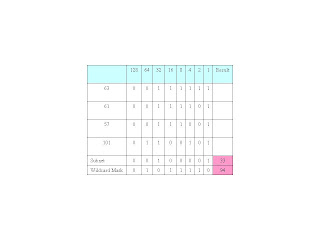
Our summary address now looks like: 100.0.33.xxx 27.55.94.xxx
Now the last octet for all addresses is zero so the subnet address must be 0 in the last octet and the wilcard mask must be 255 in the last octet.
Our completed summary address looks like: 100.0.33.0 27.55.94.255
Apply this technique as you wish, for example:
access-list 1 permit 100.0.33.0 27.55.94.255
This is a great technique for reducing something complex into easier computation so hats off to Mark again for turning me on to this.




